MPC Controller
for RoboCup SSL
Implementation of RRT* for global planning and Model Predictive Control (MPC) for local obstacle avoidance in dynamic soccer environments.
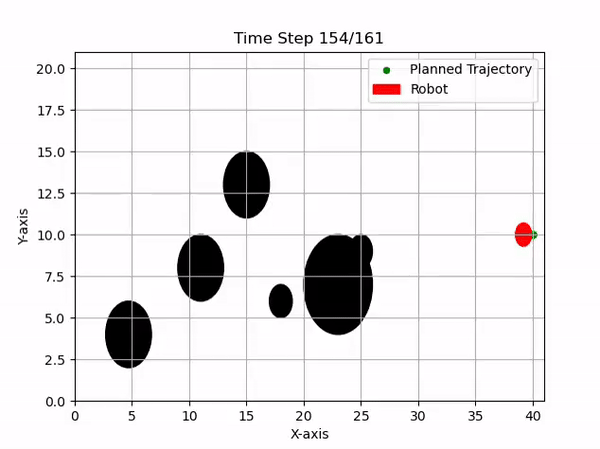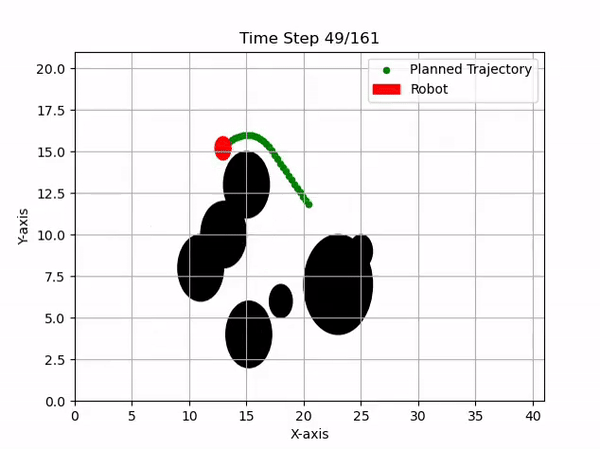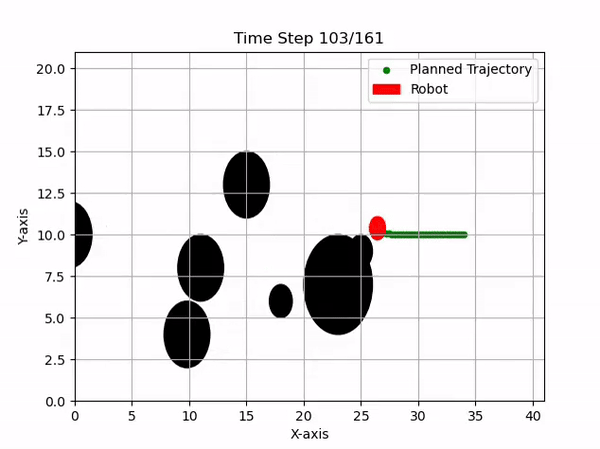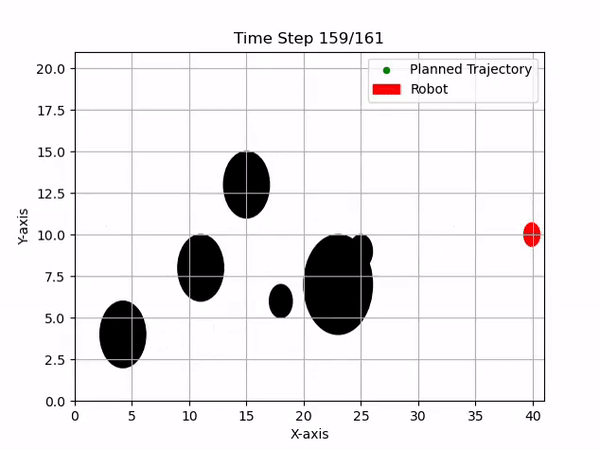
Implementation of RRT* for global planning and Model Predictive Control (MPC) for local obstacle avoidance in dynamic soccer environments.

The Delft Mercurians are a student team competing in the RoboCup Small Size League (SSL). In this fast-paced environment, robots must navigate dynamically to play soccer autonomously.
As an Infrastructure Software Developer, I focused on the navigation stack, combining Rapidly-exploring Random Tree Star (RRT*) for global path optimality and Model Predictive Control (MPC) for reactive, local obstacle avoidance and trajectory tracking.
We model the holonomic robot as a point mass in the state space. The discrete-time state space model is:
Where $\vec{x}$ is position and $\vec{u}$ is velocity input. The optimization problem minimizes tracking error and control effort:
We utilize the CasADi solver to handle these logical constraints in real-time, ensuring the robot avoids dynamic obstacles (other players) while maintaining optimal trajectory.
The integration of these algorithms contributed to the team's performance in the 2024 competition.
Team Delft Mercurians (Student Team)
Role Software Developer - Infrastructure
Tech Stack C++, ROS 2, CasADi, CMake