Small Sized League RoboCup
Implemented Path Planning on the Delft Mercurians Robots
Introduction
As a Software Developer specializing in infrastructure, I play a key role within the Delft Mercurians, a dedicated student team focused on advancing robotics technology for the RoboCup Small Size League. Specifically, I work on the path planning of the robots, implementing RRT* for the global planner and using Model Predictive Control (MPC) for local obstacle avoidance.
Path Planning Implementation
Rapidly-exploring Random Tree Star (RRT*)
For global path planning, we implemented the RRT* algorithm. This method efficiently explores the search space and finds the optimal path by incrementally building a tree of possible paths. The RRT* ensures that the paths generated are not only feasible but also optimal in terms of the cost function defined.
Model Predictive Control (MPC)
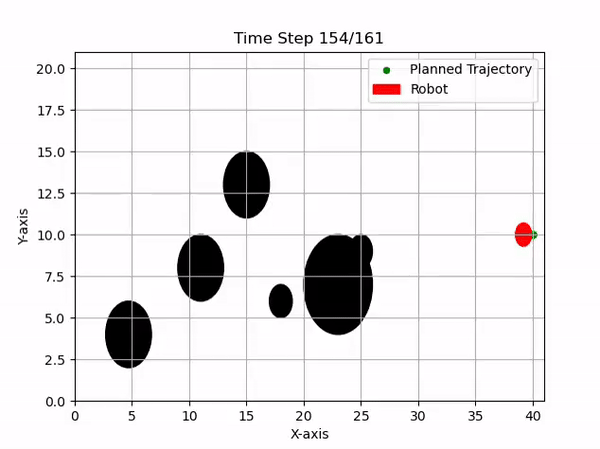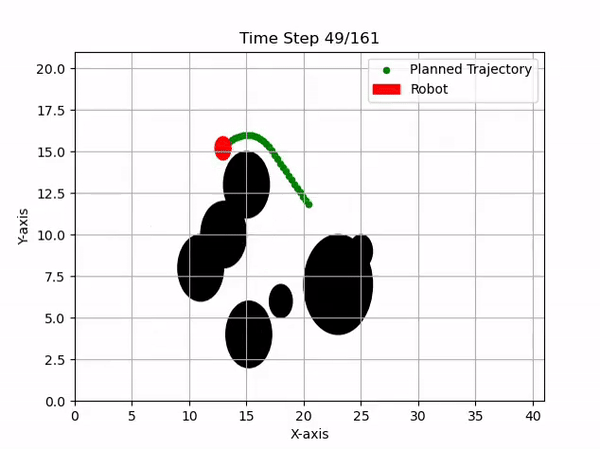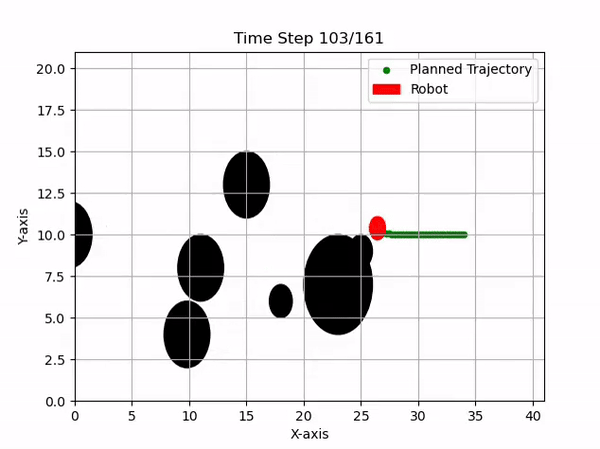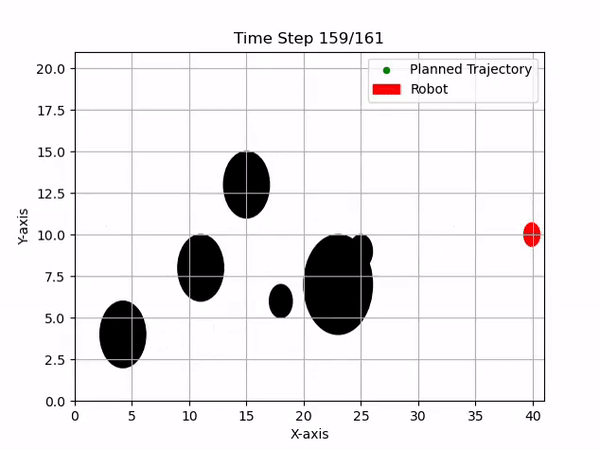
Currently, the team is integrating MPC for local obstacle avoidance. Starting with a simple 2D visualization, we implement MPC to handle dynamic environments effectively.
State Space
The first step was to determine the state space model. Given that the system is holonomic, we assumed a point mass for simplicity. The state space can be expressed as:
\[\vec{x}[k+1] = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \vec{x}[k] + T_s \cdot \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \vec{u}[k],\]where state \(\vec{x}\\) is the position in the \(x\) and \(y\) directions, \(\begin{bmatrix} x & y \end{bmatrix}^\intercal\), \(\vec{u}\) are the velocity inputs sent to the robot, \(\begin{bmatrix} v_x & v_y \end{bmatrix}^\intercal\), and \(T_s\) is the sampling time.
Cost Function and Constraints
With the state space defined, the cost function and constraints are formulated as follows:
\[J = \sum_{k=0}^{N-1} \left[ \|x_k - r_k\|_{Q}^2 + \|u_k\|_{R}^2 \right] + \|x_N - r_N\|_{Q}^2,\]where \(r_k\) and \(r_N\) are the desired positions, and \(R\) and \(Q\) are weighting matrices determining the priority of tracking error vs. control input.
The optimization problem is then defined as:
\[\begin{aligned} \min_{u_k} \quad & \sum_{k=0}^{N-1} \left[ \|x_k - r_k\|_{Q}^2 + \|u_k\|_{R}^2 \right] + \|x_N - r_N\|_{Q}^2 \\ \text{subject to} \quad & \left\| p_{r} - p_{o} \right\|_2 \geq r_r + r_o, \\ & \vec{v} \leq \vec{v}_{lim} \end{aligned}\]Obstacle Avoidance
Obstacle avoidance is achieved by adding constraints to the cost function to prevent the robot from coming into contact with obstacles. The constraint is defined as:
\[\left\| p_{r} - p_{o} \right\|_2 \geq r_r + r_o,\]where \(p_r\) and \(p_o\) are the centers of the robot and obstacle, respectively, and \(r_r\) and \(r_o\) are their radii. Additionally, velocity constraints ensure the calculated trajectory is physically achievable.
Solver
The full optimization problem is solved using the casADi solver, which is capable of handling dynamic and static environments effectively. This approach was inspired by the RoboDragons’ 2022 implementation.
Conclusion
This project demonstrates the implementation of sophisticated path planning algorithms in the RoboCup Small Size League. By combining global and local planners, the Delft Mercurians’ robots can navigate complex environments efficiently and safely.
Future Work
Future efforts will focus on refining the MPC implementation and further integrating it with real-time sensor data to enhance the robots’ responsiveness to dynamic obstacles.
Acknowledgements
I would like to thank the Delft Mercurians team for their support and collaboration throughout this project.